根据郝斌老师的视频所做的一份笔记。
视频地址:https://www.bilibili.com/video/BV11s41167h6
老师讲得清晰易懂,非常推荐用来入门数据结构。
预备知识
指针
- 指针的重要性
- 指针是C语言的灵魂
- 定义
- 地址
- 地址就是内存单元的编号
- 从0开始的非负整数
- 范围:0 - FFFFFFFF
- 地址
- 指针
- 指针就是地址 地址就是指针
- 指针变量是存放内存单元地址的变量
- 指针的本质是一个操作受限的非负整数
- 分类
- 基本类型的指针
- 指针和数组的关系
结构体
为什么会出现结构体?
- 为了表示一些复杂的数据,而普通的基本类型变量无法满足要求。
什么叫结构体
- 结构体是用户根据实际需要自己定义的复合数据类型
如何使用结构体
两种方式
1
2struct Student st = {1000, "lisi", 20};
struct Student * pst = &st;
通过结构体变量名来实现
- st.sid
通过指向结构体变量的指针来实现【重点】
- pst->sid
- pst所指向的结构体变量中的sid这个成员
注意事项
- 结构体变量不能加减乘除,但可以相互赋值
- 普通结构体变量和结构体指针变量作为函数传参的问题
1 |
|
动态内存的分配和释放
1 |
|
模块一
线性结构[把所有的结点用一根直线穿起来]
连续存储 数组
什么叫数组
- 元素类型相同,大小相等
数组优缺点优点:
- 存取速度快
缺点:
- 事先必须知道数组的长度
- 插入删除元素很慢
- 空间通常是有限制的
- 需要大块连续的内存块
数组的算法
1 |
|
离散存储 链表
定义
- n个节点离散分配
- 彼此通过指针相连
- 每个节点只有一个前驱节点,每个节点只有一个后续节点
- 首节点没有前驱节点,尾节点没有后续节点
链表优缺点
优点:
- 空间没有限制
- 插入删除元素很快
缺点:
- 存取数据很慢
专业术语
- 首节点
- 第一个有效节点
- 尾节点
- 最后一个有效节点
- 头结点
- 头节点的数据类型和首节点类型一样
- 第一个有效节点之前的那个节点
- 头节点并不存放有效数据
- 加头节点的目的主要为了方便对链表的操作
- 头指针
- 指向头节点的指针变量
- 尾指针
- 指向尾节点的指针变量
如果希望通过一个函数来对链表进行处理,我们至少要接收链表的哪些参数?
只需要一个参数:头指针
因为我们通过头指针可以推算出链表的其他所有参数
1 |
|
分类
- 单链表
- 双链表
- 每个节点有两个指针域
- 循环链表
- 能通过任何一个节点找到其他节点
- 非循环链表
算法
遍历
查找
清空
销毁
求长度
排序
删除节点
1
2
3
4p->pNext = p->pNext->pNext; // 存在内存泄露问题
r = p->pNext;
p->pNext = p->pNext->pNext;
free(r);插入节点
1
2q->pNext = p->pNext;
p->pNext = q;创建单链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
typedef struct Node{
int data;// 数据域
struct Node * pNext; // 指针域
}NODE, *PNODE;
PNODE create_list(void);
void traverse_list(PNODE pHead);
int main(void){
// 存放链表头结点
PNODE pHead;
// 创建链表
pHead = create_list();
// 遍历链表
traverse_list(pHead);
return 0;
}
PNODE create_list(void){
PNODE pHead = (PNODE)malloc(sizeof(PNODE));
int len; // 节点个数
int val;
if(pHead == NULL){
printf("动态创建内存失败!");
exit(-1);
}
PNODE pTail = pHead;
pTail->pNext = NULL;
printf("请输入生成链表节点个数:\n");
scanf("%d", &len);
for(int i=0; i<len; ++i){
printf("请输入第%d个节点的值:\n", i+1);
scanf("%d", &val);
// 创建节点
PNODE pNode = (PNODE)malloc(sizeof(PNODE));
if(pNode==NULL){
printf("动态创建内存失败!");
exit(-1);
}
//
pNode->data = val;
//
pTail->pNext = pNode;
// 给pNode->pNext 设置为尾结点
pNode->pNext = NULL;
// 改变地址引用
pTail = pNode;
// 问题:pTail = pNode这里会不会覆盖掉 pTail->pNext = pNode的赋值?
// 不会, pTail->pNext = pNode 是已经赋值完成,这里是将 pNode 地址赋值给 pTail
// 并不会改变pTail->pNext 的值
}
return pHead;
}
void traverse_list(PNODE pHead){
PNODE p = pHead->pNext;
while(p != NULL){
printf("%d ", p->data);
p = p->pNext;
}
return;
}单链表的算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
typedef struct Node{
int val;// 数据域
struct Node * pNext; //指针域
}NODE,*PNODE;
PNODE create_list();
void traverse_list(PNODE pHead);
bool is_empty(PNODE pHead);
int length_list(PNODE pHead);
void sort_list(PNODE pHead);
bool insert_list(PNODE pHead, int pos, int val);
bool delete_list(PNODE pHead, int pos, int *pVal);
int main(void){
// 创建链表
PNODE pHead = create_list();
// 遍历链表
traverse_list(pHead);
// 插入节点
insert_list(pHead, 4, 100);
traverse_list(pHead);
// 删除节点
int pVal;
if(delete_list(pHead, 5, &pVal)){
printf("删除成功,删除数据为%d\n", pVal);
} else{
printf("删除失败!");
}
traverse_list(pHead);
// 判断链表是否为空
/*
if(is_empty(pHead)){
printf("链表为空!\n");
}else{
printf("链表不为空!\n");
} */
// 返回链表长度
/*
int len = length_list(pHead);
printf("链表长度为:%d\n", len);
*/
// 对链表进行排序
//sort_list(pHead);
//traverse_list(pHead);
return 0;
}
// 创建链表
PNODE create_list(){
PNODE pHead = (PNODE)malloc(sizeof(NODE));
int len;
int val;
if(NULL == pHead){
printf("内存分配失败!\n");
exit(-1);
}
PNODE pTemp = pHead;
pTemp->pNext = NULL;
printf("请输入创建链表节点数:\n");
scanf("%d", &len);
for(int i=0; i<len; i++){
printf("请输入第%d个节点的值:\n", i+1);
scanf("%d", &val);
// 创建节点
PNODE pNew = (PNODE)malloc(sizeof(NODE));
pNew->val = val;
pTemp->pNext = pNew;
pNew->pNext = NULL;
pTemp = pNew;
}
return pHead;
}
// 遍历列表
void traverse_list(PNODE pHead){
PNODE p = pHead->pNext;
while(NULL != p){
printf("%d ", p->val);
p = p->pNext;
}
printf("\n");
return;
}
// 判断链表是否为空
bool is_empty(PNODE pHead){
if(NULL == pHead->pNext)
return true;
else
return false;
}
// 返回链表长度
int length_list(PNODE pHead){
PNODE p = pHead->pNext;
int len = 0;
while(NULL != p){
len ++;
p = p->pNext;
}
return len;
}
// 链表排序
void sort_list(PNODE pHead){
/*
for(i=0;i<4;i++){
for(j=i+1;j<4-i;j++){
if(arr[i]>arr[j]){
t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}*/
PNODE q,p;
int i,j,t;
int len = length_list(pHead);
for(i=0,p=pHead->pNext; i<len; i++, p=p->pNext){
for(j=i+1;j<len;j++){
if(p->val > p->pNext->val){ // arr[i]>arr[j]
t = p->val; // t = arr[i]
p->val = p->pNext->val; // arr[i] = arr[j]
p->pNext->val = t; // arr[j] = t
}
}
}
}
// 链表节点插入
bool insert_list(PNODE pHead, int pos, int val){
int i = 0;
PNODE p = pHead;
while(NULL!=p&&i<pos-1){
p = p->pNext;
++i;
}
if(i>pos-1||NULL==p)
return false;
// 实现插入节点
PNODE pNew = (PNODE)malloc(sizeof(NODE));
if(NULL==pNew){
printf("动态分配内存失败!\n");
exit(-1);
}
pNew->val = val;
PNODE q = p->pNext; // 将下一个节点得指针 赋值给临时指针q
p->pNext = pNew; // 将下一节点的指针指向新生成的节点
pNew->pNext = q; // 再将新生成的节点的指针域指向临时指针q
return true;
}
// 节点删除
bool delete_list(PNODE pHead, int pos, int * pVal){
PNODE p = pHead;
int i = 0;
while(NULL!=p->pNext&&i<pos-1){
p = p->pNext;
i++;
}
if(i>pos-1||NULL==p->pNext){
return false;
}
// 实现删除节点
PNODE q = p->pNext;
*pVal = q->val;
p->pNext = p->pNext->pNext;
free(q);
return true;
}
线性结构->栈
定义
一种可以实现”先进后出”的存储结
栈类似于箱子
分类
- 静态栈
- 动态栈
算法
- 出栈
- 入栈
应用
- 函数调用
- 中断
- 表达式求值
- 内存分配
- 缓冲处理
- 迷宫
栈算法
1 |
|
线性结构->队列
定义
- 一种可以实现“先进先出”的存储结构
分类
- 链式队列
- 用链表实现
- 静态队列
- 用数组实现
- 静态队列通常必须是循环队列
静态队列为什么必须是循环队列
循环队列需要几个参数来确定
- front
- real
循环队列各个参数的含义
- 2个参数不同场合有不同的含义
- 队列初始化
- front 和 real 的值都是零
- 队列非空
- front代表的是队列的第一个元素
- rear代表的是队列的最后一个有效元素的下一个元素
- 队列空
- font 和 real的值相等,但不一定是零
- 队列初始化
- 2个参数不同场合有不同的含义
循环队列入队伪算法讲解
两步完成
将值存入r所代表的位置
错误的写法 r = r+1
- 正确的写法 r = (r+1)%数组的长度
循环队列出队伪算法讲解
- front = (front+1)%数组的长度
如何判断循环队列是否为空
- 如果front与real的值相等,则该队列就一定为空
如何判断循环链表是否已满
预备知识
front的值可能比rear大
front的值也可能比real小
当然也可能两者相等
两种方式
多增加一个表标识参数
少用一个元素【通常使用第二种方式】
如果r和f值紧挨着,则队列已满
1
2
3
4
5// C语言伪算法表示:
if((r+1)%数组长度 == f)
已满
else
未满
队列的算法
- 入队
- 出队
队列的具体应用
- 所有和时间有关的操作都有队列的影子
循环队列的实现
1 |
|
专题->递归
定义
- 一个函数自己直接或间接调用自己
递归满足三个条件
- 递归必须得有一个明确的中止条件
- 该函数所处理的数据规模必须在递减
- 这个转化必须是可解的
循环和递归
递归
- 易于理解
- 速度慢
- 存储空间大
循环
- 不易理解
- 速度慢
- 存储空间小
使用递归的例子
- 求阶乘
- 1+2+3+4+…100的和
- 汉诺塔
- 走迷宫
递归的应用
- 树和森林就是以递归的方式定义的
- 树和图的很多算法都是以递归来实现的
- 很多数学公式就是以递归的方式定义的
模块二:非线性结构
树
树定义
- 专业定义
- 有且只有一个称为根的节点
- 有若干个互不相交的子树,这些子树本身也是一颗树
- 通俗定义
- 树是由节点和边组成
- 每个节点只有一个父节点但是可以有多个子节点
- 但有一个节点例外,该节点例外,该节点没有父节点,此节点称为根节点
专业术语
节点 父节点 字节点
子孙 堂兄弟
深度
从根节点到最底层节点的层数称为深度
根节点是第一层
叶子节点
没有子节点的节点
非终端节点
实际就是非叶子节点
度
子节点的个数称为度
树分类
- 一般树
- 任意一个节点的子节点的个数都不受限制
- 二叉树
- 任意一个节点的子节点个数最多两个,且子节点的位置不可更改
- 分类
- 一般二叉树
- 满二叉树
- 在不增加树的层数前提下,无法再多添加一个节点的二叉树就是满二叉树
- 完全二叉树
- 如果只是删除了满二叉树最底层最右边的连续若干个节点,这样形成的二叉树就是完全二叉树
- 森林
- n个互不相交的树的集合
树的存储
二叉树的存储
- 连续存储【完全二叉树】
- 优点
- 查找某个节点的父节点和子节点(也包括判断有没有父节点和子节点)速度很快
- 缺点
- 耗用内存空间
- 优点
- 连续存储【完全二叉树】
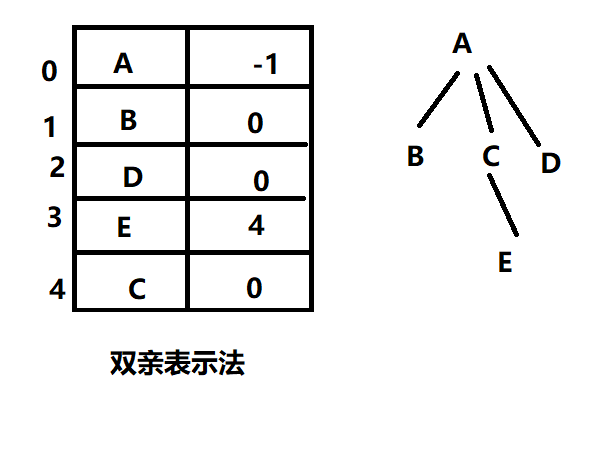
一般树存储
双亲表示法
求父节点方便
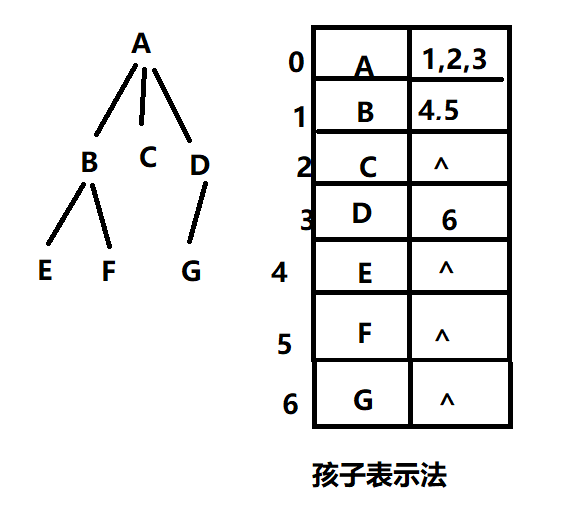
孩子表示法
- 求子节点方便
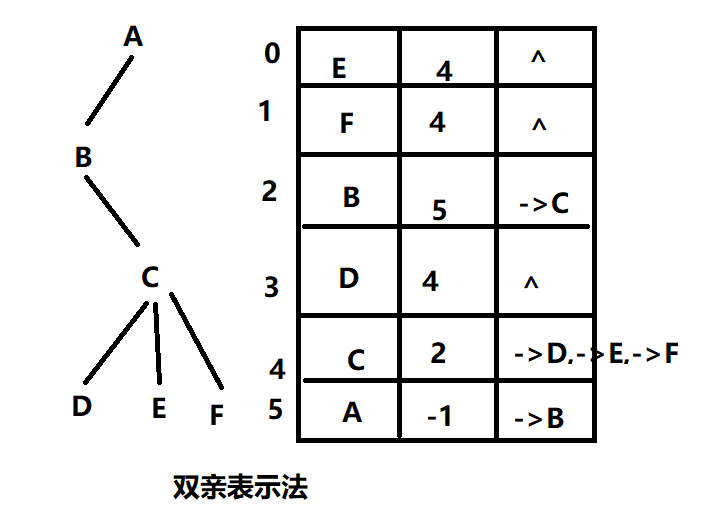
双亲孩子表示法
- 求父节点和子节点都很方便
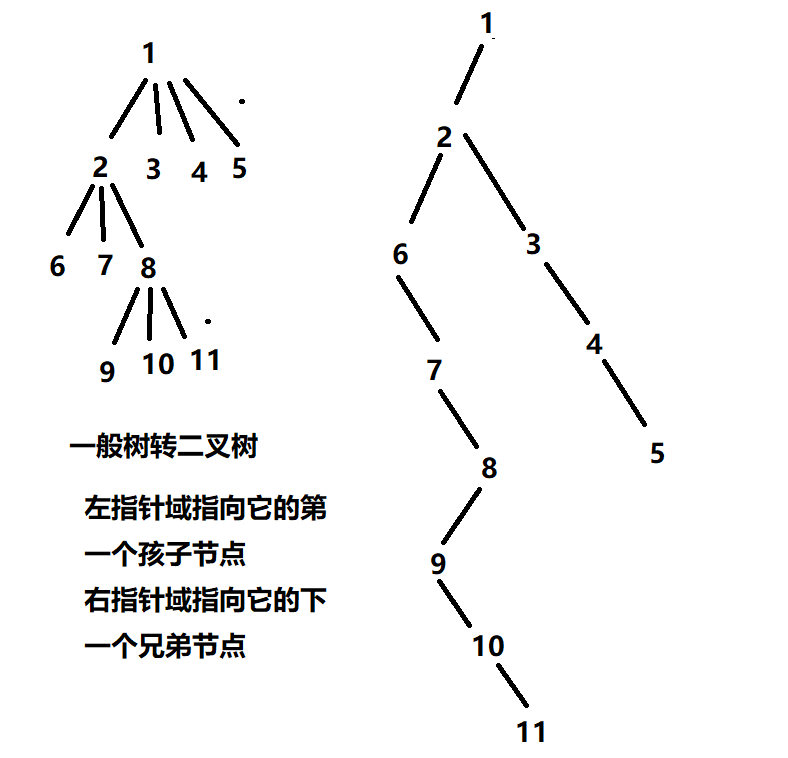
二叉树表示法
把一个普通树转化成二叉树来存储
1
2
3
4
5
6具体转换方法:
设法保证任意一个节点的
左指针域指向它的第一个孩子节点
右指针域指向它的下一个兄弟节点
只要能满足此条件,就可以把一个普通树转化成为二叉树
一个普通树转化成的二叉树一定没有右子树
森林的存储
- 先把森林转化为二叉树,再存储二叉树。
二叉树操作
遍历
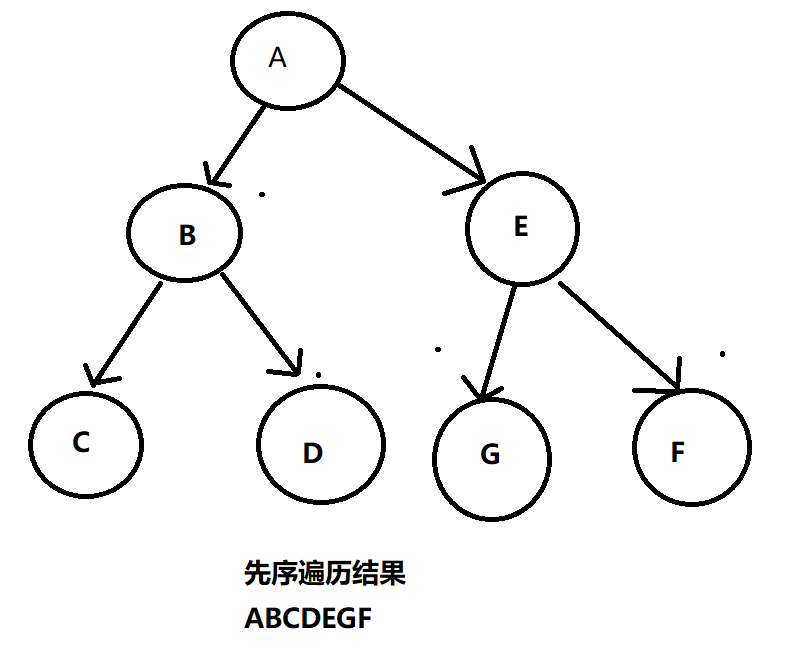
先序遍历
1
2
3先访问根节点
再先序访问左子树
再先序访问右子树
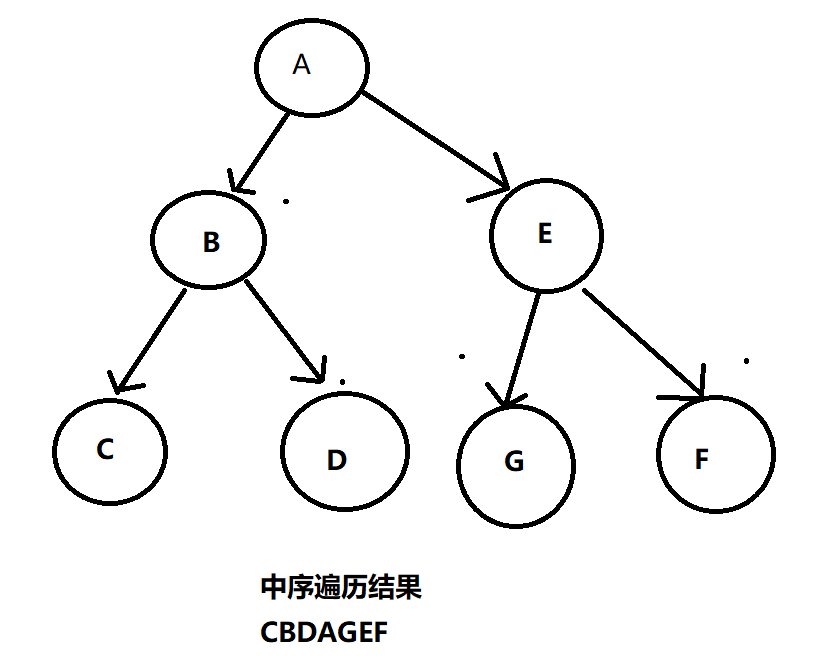
中序遍历
1
2
3先中序遍历左子树
再访问根节点
再中序遍历右子树
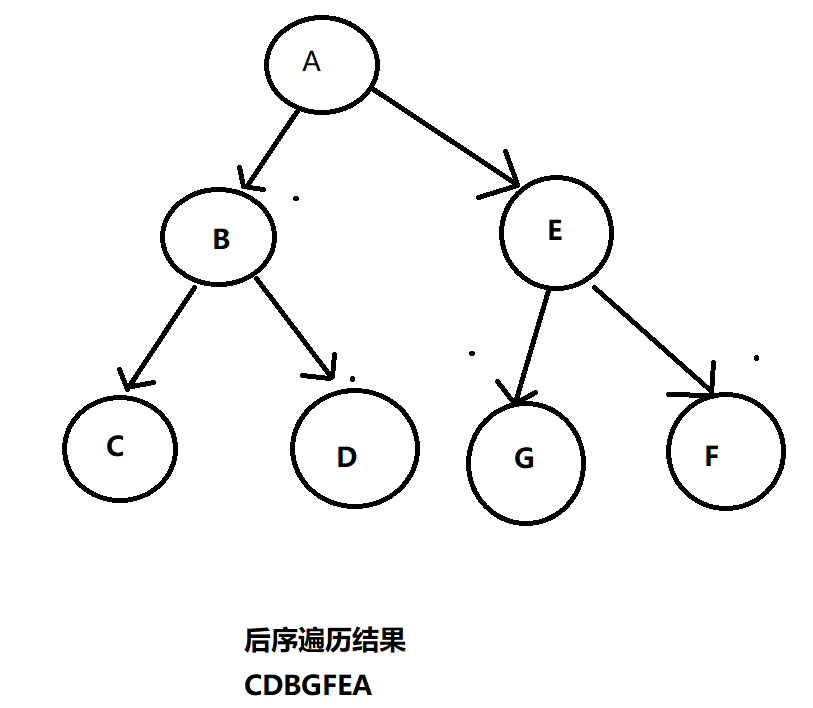
后序遍历
1
2
3先中序遍历左子树
再中序遍历右子树
再访问根节点
已知两种遍历序列求原始二叉树通过 先序遍历 和 中序遍历 或者 中序遍历 和后序遍历 我们可以还原出原始二叉树
但是通过先序遍历 和 后续遍历 无法还原出原始二叉树
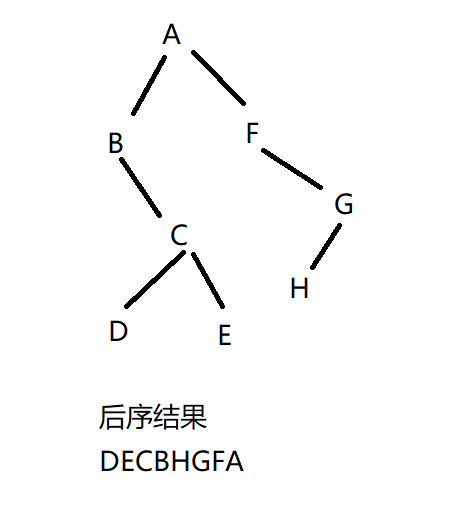
已知先序和中序求后序
1
2
3先序:ABCDEFGH
中序:BDCEAFHG
求后序:?
 |
|---|
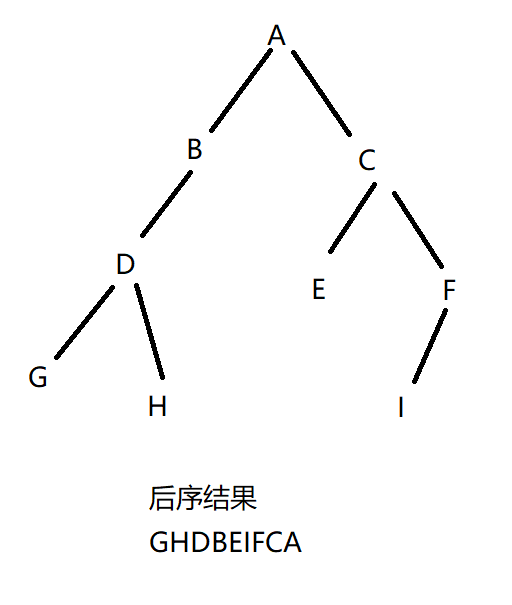
1 | 先序:ABDGHCEFI |
已知中序和后序求先序
1 | 中序:BDCEAFHG |
图
待学习…
排序算法
冒泡排序
实现代码
1 |
|
1 |
|
快速排序
原理图
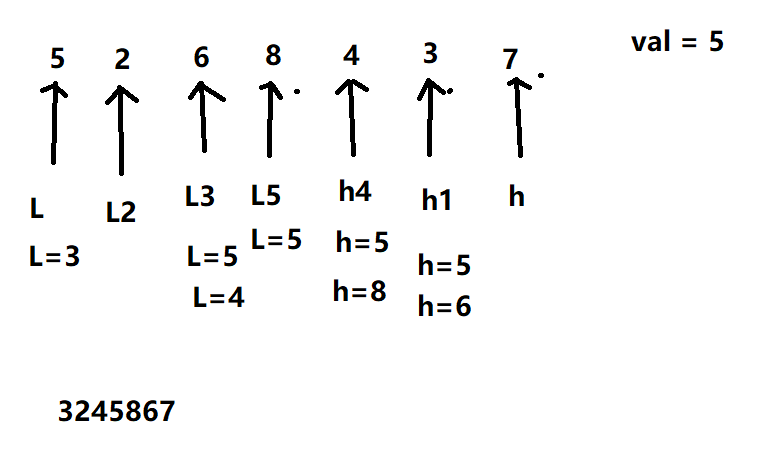 |
|---|
实现代码
1 |
|
插入排序
选择排序
归并排序
查找算法
待学习…